It’s time we thought again about quantum theory. There’s nothing actually wrong with the theory itself—it works fantastically well for understanding how atoms and subatomic particles behave.
The problem is how we talk about quantum theory. We keep insisting that it’s weird: waves becoming particles, things being in two places (or two states) at once, spooky action at a distance, that sort of thing. Isn’t it perverse to clothe in mystery a theory that scientists use routinely to understand the world?
Part of the issue is that everyday objects are discrete, localized, and unambiguous, and so, very different to quantum objects. But why is that the case? Why is our everyday world always “this or that” and never “this and that”? Why, as things get bigger, does quantum physics turn into classical physics, governed by laws like those that Isaac Newton wrote down over three centuries ago?
This switch is called the quantum-classical transition, and it has puzzled scientists for many decades. We still don’t completely understand it. But over the past two or so decades, new experimental techniques have pushed the transition to ever-larger sizes. Most scientists agree that technical difficulties will prevent us from ever putting a basketball, or even a human, in two places at once. But an emerging understanding of the quantum-classical transition also suggests that there is nothing in principle that prohibits it—no cosmic censorship separates our “normal” world from the “weird” world that lurks beneath it. In other words, the quantum world may not be so weird after all.
Imagine a broken drying machine that spits out pairs of unmatched socks. They come in complementary contrasts: if one is red, the other is green. Or, if one is white, the other is black, and so on. We don’t know which of these options we’ll get until we look—but we do know that if we find one is red, we can be sure the other is green. Whatever the actual colors are, they are correlated with one another.
Now imagine the quantum mechanical version of this same machine. According to the Copenhagen interpretation of quantum mechanics developed in the mid-1920s by Niels Bohr, Werner Heisenberg, and collaborators, quantum socks in a correlated state (where the color of one is linked to the color of the other) don’t actually have any fixed colors until we look. The very act of looking at one quantum sock determines the color of the other. If we look in one way, the first sock might be red (and the other therefore green). If we look in another, the first is white (and the other black).
Crudely, you could say that in these correlated pairs the colors of the socks are characteristics that extend well beyond the socks themselves. The color of a given sock is not local, that is, not contained in the properties of just that one sock. The two colors are said to be entangled with each other.
Decoherence bleeds away discord. Quantum phenomena are converted to ones that obey classical rules.
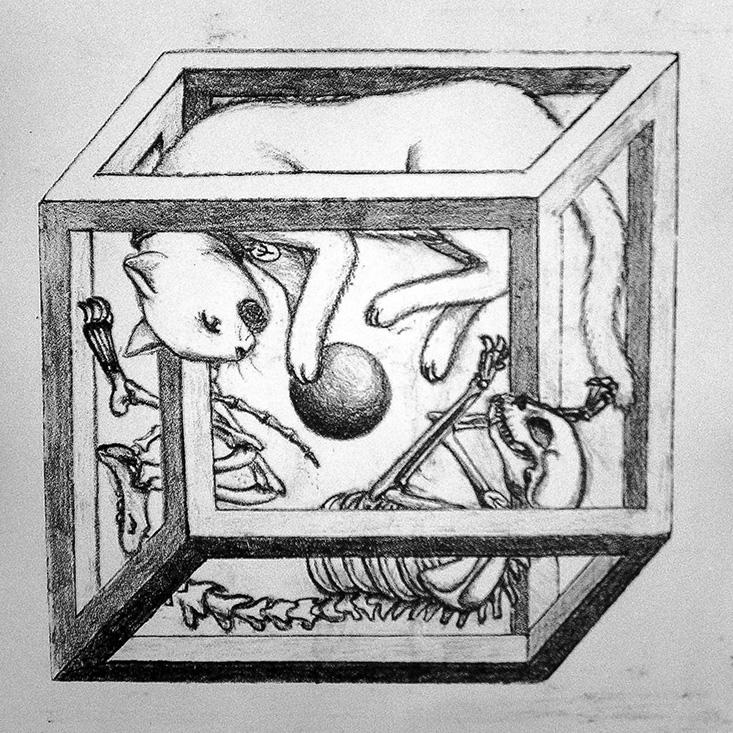
The physicist Erwin Schrödinger described entanglement as the key to quantum behavior, and used it to construct a famous paradox. It begins with an unfortunate cat that Schrödinger imagined trapped inside a box, into which a lethal poison was released by the outcome of some quantum event. Because the event was quantum, it could be in what physicists call a superposition state: both triggering the poison release, and not triggering it.
These superpositions are not unusual for tiny objects like atoms that are firmly in the quantum realm. But, because Schrödinger entangled the event with a large cat, the result is the paradoxical conclusion that the cat is both killed and not killed.
The conventional resolution to the paradox was to claim that making a measurement on a superposition state, like the live–dead cat, forces a choice, so that the superposition collapses the cat—indeed, in effect the whole universe—into one state or another: The cat is either dead or alive, but not both. In that view, we can never see the live–dead cat.
But what was the state of the cat before we looked? According to the Copenhagen interpretation, the question has no meaning. Reality, it maintains, is what we can observe and measure, and it makes no sense to wonder about what things are really like before we make those observations.
Others, most prominently Albert Einstein, couldn’t accept this. They stuck with the classical “realist” view, which says that everything has particular, objective properties, whether we look or not. Einstein and two young colleagues, Boris Podolsky and Nathan Rosen, came up with a version of the “quantum drying machine” thought experiment to try to demonstrate how quantum theory led to a paradox, in which a measurement in one place instantly affected an object in another place. But in the 1980s, measurements of laser photons showed that entanglement really does work that way—not because of “faster-than-light” communication, but because quantum properties can be genuinely non-local, spread over more than one particle.
Since then, experimentalists have been working on building ever-larger quantum objects, which are big compared with atoms but small compared with real cats. They are often called “Schrödinger’s kittens,” and they are rapidly growing up.

One key to these kittens becoming cats has been learning how to maintain quantum coherence, or roughly, the ability for the peaks and troughs of wave-like quantum particles to stay synchronized. As a quantum state evolves, it gets entangled with its environment, and quantum coherence can leak away into the surroundings. One might very crudely imagine it to be a little like the way heat in a hot body gets dissipated into a cooler surrounding environment.
Another way to think of it is to say that information gets increasingly local. The point about quantum systems is that non-local correlations mean you can’t know everything about some part of it by making measurements just on that part. There’s always some residual ignorance. In contrast, once we have established that a sock is red or green, there’s nothing left to be known about what color it is. Wojciech Zurek of Los Alamos National Laboratory in New Mexico has formulated an expression for the ignorance that remains once the state of the measuring apparatus has been determined, which he calls quantum discord. For a classical system, the discord is zero. If it is greater than zero, the system has some quantumness to it.
Decoherence bleeds away discord. Quantum phenomena are converted to ones that obey classical rules: no superpositions, no entanglement, no non-locality, and a time and a place for everything.
How big, then, can quantum systems get before decoherence starts to destroy their quantumness? We have known that very small particles like electrons can behave as coherent quantum waves ever since the groundbreaking observation of electron interference in the late 1920s. Soon after, the wavelike properties of entire atoms were demonstrated. But it wasn’t until the 1990s, when it became possible to create coherent “matter waves,” that quantum wave interference was observed for atoms and molecules.
Decoherence and coarse-graining of measurements offer two complementary routes to the classical world.
How big can these chunks of matter get while still undergoing interference? In 1999 a team at the University of Vienna led by Anton Zeilinger and Markus Arndt marshaled 60-atom carbon molecules called fullerenes (C) into a beam, passed it through a grating of slits spaced 100 nanometers apart and made from the ceramic silicon nitride, and detected an interference pattern on the far side. Arndt and his coworkers have now demonstrated that this quantum waviness persists for tailor-made organic molecules containing 430 atoms and up to 6 nanometers across: easily big enough to see in an electron microscope and comparable to the size of small proteins. The interference patterns can be washed out by decoherence: They vanish as the researchers admit gas into the apparatus, increasing the interactions of the molecules with their environment.
Because this interference depends on the molecules being in superposition states—in effect, each passes through more than one slit at a time—the molecules can be thought of as molecular Schrödinger’s kittens. They’re still very tiny, though, and obviously not alive. Might it be possible to push up the size scale to that at which life becomes possible—for example, to look for interference in “Schrödinger’s viruses?”
That idea has been proposed by Ignacio Cirac and Oriol Romero-Isart at the Max Planck Institute for Quantum Optics in Garching, Germany. They have outlined an experimental method for preparing superposition states not only for viruses (with sizes of around 100 nanometers or more) but also for extremely hardy microscopic creatures called tardigrades or water bears (which are up to 1 millimeter or so in size). These objects would be levitated in an optical trap made of intense laser-light fields and then coaxed into a superposition of their vibrational states within the trapping force field (like balls rolling back and forth in the bottom of a bowl). Tardigrades have been shown to survive on the outside of spacecraft, and so might withstand the rigors of a high-vacuum experiment like this. So far, however, it’s just a proposal.
We know already, however, that objects large enough to see with the naked eye can be placed in entangled stages. A team led by Ian Walmsley, a physicist at the University of Oxford, achieved this in 2011 using laser pulses to excite entangled quantum vibrations (phonons) in two diamond crystals 3 millimeters wide and 15 centimeters apart. Each phonon involves the coherent vibration of about 1016 atoms, corresponding to a region of the crystal measuring about 0.05 by 0.25 millimeters. To create the superposition, the researchers first placed a laser photon in an entangled state by using a beam splitter to send it toward either diamond with equal probability. So long as they don’t detect this path, the photon creates an entangled vibration in both crystals. When a phonon is excited, it emits a secondary photon, which the researchers could detect without finding out which crystal it comes from. In that case the phonon must be considered non-local, in a sense embracing both diamonds.
Another way to look at quantum effects in relatively large systems is to study the vibrations of very small springy structures like nanometer-scale cantilevers and other “nanomechanical resonators.” At the scale of molecules, vibrations are quantized: They can only occur at well-defined frequencies, or in mixed superpositions of these allowed quantum states. Nanomechanical resonators are also small and light enough to have, in theory, distinguishable quantized vibration states. An ideal way to read out the vibrational state of the resonating element is to couple its mechanical motion to light, an approach called optomechanics. In its simplest form, this might involve making a chamber in which light can bounce back and forth between mirrors, with one of the mirrors attached to a spring so that it can oscillate.
Several groups have now demonstrated quantum behavior in such nanoscale optomechanical systems. John Teufel and his coworkers at the National Institute of Standards and Technology in Boulder, Colorado, for example, used a drum-like aluminum membrane 100 nanometers thick and 15 micrometers (μm) wide as the resonator, coupled to a microwave-frequency cavity, while Oskar Painter and colleagues at the California Institute of Technology in Pasadena used a thin silicon beam 15 micrometers long, with a 600 by 100 nanometer cross-section, clamped at both ends. You need a microscope to see those objects, but they’re immense compared with molecules. To ensure that their oscillators stayed in a single, lowest-energy vibrating state, both teams chilled their devices close to absolute zero using cryogenics, and then used laser beams or microwaves to reduce the temperature even further.
If you want to generate quantum effects such as superpositions and entanglement in these resonators, you need to be able to control their quantum behavior. One way to do this is to couple the resonators to a quantum object whose state can be switched at will, such as a two-state “quantum bit” of the kind being used to build quantum computers. Andrew Cleland of the University of California at Santa Barbara and his coworkers achieved this for a microscopic sheet of aluminum nitride. Others are hoping to prepare oscillators in superposition states and then watch how they decohere as they get entangled with their environment: middle-sized Schrödinger kittens bouncing in the void.

If we could totally suppress decoherence, would that get us all the way to a full-size Schrödinger cat? It might not be that simple. This is because, to know that you’d made one, you’d have to look at it. Sure, the act of entangling a system with a measuring apparatus could itself decohere it—but the problem might be even worse than that. Physicists Johannes Kofler, now at the Max Planck Institute for Quantum Optics in Garching, and Caslav Brukner of the University of Vienna proposed in 2007 that the very act of studying a large quantum system experimentally may induce the emergence of classical behavior even without any decoherence. Measurement itself can turn quantum multiplicity into classical uniqueness.
This, say Kofler and Brukner, is because measurements can’t be infinitely precise. The argument is often made in textbooks that the limits of experimental resolution prevent us from being able to see quantum discreteness in a macroscopic system: Because the discrete energy states get ever closer as the size of the system increases, they seem to blur into the continuum of energies that we perceive in, say, a moving tennis ball. But that can’t be the only reason why tennis balls are “classical,” because it doesn’t actually eliminate the quantumness of the object—forbidding, for example, a superposition of tennis-ball velocities.
Kofler and Brukner showed that, when a measurement is “coarse-grained,” so that the resolution is insufficient to distinguish several closely spaced quantum states of a very large system, the quantum-mechanical equations describing how it evolves in time collapse into the classical equations of mechanics devised by Isaac Newton. “We can rigorously show that under the coarse-grained measurements, entanglement or nonlocal features of many-particle states are washed out,” says Brukner. Classical physics emerges from quantum physics when measurement becomes fuzzy, as it always must for “big” systems: ones composed of many particles with many possible states.
Some researchers have argued that a superposition could persist in the nerve signal sent from the retina to the brain, so that fleeting “perceptual superpositions” are possible.
The argument is not airtight: It’s possible in principle (though extremely hard in practice) to create exotic situations in which the coarse-graining of measuring some property of the system doesn’t ensure classicality. But Hyunseok Jeong of Seoul National University in South Korea and his collaborators have shown that even here there’s an aspect of measurement that destroys quantum behavior. In addition to some inevitable fuzziness in what we measure, says Jeong, there is also a degree of ambiguity about exactly when and where we measure: what he calls the measurement references. This too has the effect of making a quantum system appear to behave like a classical one.
Kofler says that decoherence and coarse-graining of measurements offer two complementary routes to the classical world. “If you have sufficiently strong decoherence, you get classicality independent of your measurements,” he says. “And if you have coarse-grained measurement, you get classicality independent of the interaction with the environment.”
This picture offers a striking resolution of the Schrödinger’s cat puzzle. We could never see it in a live–dead superposition, Brukner says, not because it can’t exist as such, or because of decoherence, but because, well, we just couldn’t actually see it. “Even if somebody would prepare a Schrödinger-cat state in front of us, we would not be able to reveal it as such without having an instrument of sufficient precision.” That’s to say, any measurement we could actually make on the cat wouldn’t show anything that couldn’t equally be explained by a classical picture. Even for the oscillators of optomechanical devices, detecting genuine superposition states will be challenging, involving positional differences of just fractions of an ångstrøm (10-10 meters). For such reasons, “it is quite challenging to test these ideas in a real experiment,” Jeong admits. Even so, he optimistically adds, “I hope to see my idea be tested in a laboratory in the near future.”
There are other arguments, too, for why decoherence isn’t the whole explanation for the quantum-classical transition. In the 1980s and 1990s the eminent mathematical physicist Roger Penrose, and independently the Hungarian physicist Lajos Diósi, suggested that quantum behavior of mechanical systems might also be disrupted by gravity. If that’s so, it means that classical behavior is bound to manifest itself at a certain mass limit even if you could entirely suppress decoherence—because there is never any hiding from gravity. When one object “feels” the position of the other via gravity, it amounts to a kind of measurement that can destroy the quantum coherence.
Some researchers, such as Markus Aspelmeyer at the University of Vienna and Dirk Bouwmeester at the University of California at Santa Barbara, are hoping to test this type of decoherence using optomechanics. Among the proposals, Aspelmeyer and colleagues want to conduct an experiment called MAQRO on a space satellite in zero gravity, where they could very sensitively probe matter-wave interference of particles about 100 nanometers across (huge in quantum terms) as they undergo free fall. Some theories, such as the gravitational-collapse idea of Penrose and Diósi, predict that for large enough particles the interference should vanish.
Very recently, physicist Roman Schnabel of the University of Hamburg outlined another experimental test of gravity-induced decoherence. It would involve two large mirrors, weighing 100 grams each and attached to springs that let them oscillate, that become entangled with light beams bouncing between them, so that entanglement in the light (which is relatively easy to arrange) can be converted into entanglement of the two mirrors. By switching off the light and watching how the mirrors’ oscillations evolve over the ensuing microseconds, it would be possible to look for quantum correlations between them, and to search for deviations of the decoherence rate beyond that predicted by standard quantum theory owing to gravitational effects.
There’s no doubt that strictly quantum-mechanical effects can be seen at the macroscale: Both superfluidity, when an ultracold fluid flows with no viscosity, and superconductivity, when a material carries an electrical current without resistance, are examples of that. And in a sense pretty much everything we experience, from vision to the solidity of objects, depends on effects that only quantum physics can explain.
But what seem to us to be the real peculiarities of quantum physics (entanglement and superpositions, or in other words retaining quantum discord) are another matter. There is a chance we may not need to scale these effects up to large sizes to see them: The human eye can register just three or so photons, and physicists at the University of Illinois, Urbana-Champaign, are hoping to find out how the brain responds to photons in a superposition or entangled state. Some researchers have argued that such a superposition could persist in the nerve signal sent from the retina to the brain, so that fleeting “perceptual superpositions” are possible.
Still, engineering entanglement and superposition into macroscopically large systems remains an important goal, even if it’s a distant one. Putting large systems in Schrödinger’s cat states isn’t just a question of seeing whether curiosity really does kill/not kill the cat. There would be practical benefits too: Quantum computers, which use quantum effects to give a huge boost to processing power, will need to achieve the entanglement and superpositions of large numbers of quantum bits to be practical. So understanding how decoherence kicks in as the scale increases, and finding ways to suppress it, is one of the keys to a viable quantum information technology.
More and more, though, physicists seem to be concluding that the roadblocks to real-life Schrödinger cats are technical, not fundamental. For now, that distinction might not matter much, because of the limits on what an experiment can realistically attain. “I think, it is practically impossible to completely suppress decoherence of macroscopic superpositions or entanglement,” says Jeong. “And even if you could, another enemy—coarsening of measurements—might be waiting to kill macroscopic quantum superpositions.” But he thinks that, if we were ever to develop instruments fine enough, and systems isolated enough, there’s no reason to suppose that quantum effects wouldn’t survive to human-size scales. So far, nothing we have discovered about objects in the middle ground between micro and macro contradicts that view.
For 2,000 years we have assumed that Plato’s common-sense view in the Republic applies to our tangible world: “The same thing cannot ever act or be acted upon in two opposite ways, or be two opposite things, at the same time.” Now we’re not so sure. With Schrödinger’s kittens growing up, weird isn’t what it used to be.
Philip Ball is the author of Invisible: The Dangerous Allure of the Unseen and many books on science and art.